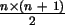 zur Berechnung der natürlichen Zahlen von 1 bis n
angewandt werden. Hier ist n allerdings n - 1. Eingesetzt und aufgelösst ergibt sich somit
zur Berechnung der natürlichen Zahlen von 1 bis n
angewandt werden. Hier ist n allerdings n - 1. Eingesetzt und aufgelösst ergibt sich somit
 ; eine Anzahl der Arbeitsschritte für den einfachen BubbleSort. Da jedoch die quadratische Komponente
der Formel überwiegt und bei grossen n massgebend ist, wird bei der Angabe der Laufzeitkomplexität
eines Algorithmus nur die entscheidende Grösse angegeben. Um diese Vereinfachung der Angabe zu signalisieren,
notiert man die Laufzeit in der O (sprich: BIG O) Notation. Fü den BubbleSort ergibt sich so
eine Laufzeitkomplexität von
; eine Anzahl der Arbeitsschritte für den einfachen BubbleSort. Da jedoch die quadratische Komponente
der Formel überwiegt und bei grossen n massgebend ist, wird bei der Angabe der Laufzeitkomplexität
eines Algorithmus nur die entscheidende Grösse angegeben. Um diese Vereinfachung der Angabe zu signalisieren,
notiert man die Laufzeit in der O (sprich: BIG O) Notation. Fü den BubbleSort ergibt sich so
eine Laufzeitkomplexität von 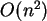 .
.
Wie einige einfache Tests durch ein kleines C-Programm ergaben, spiegelt sich die Laufzeitkomplexitä in der folgenden Tabelle wieder. Die einzelnen Tests wurden immer auf der gleichen Datenmenge durchgeführt, sie wurde lediglich um weitere Elemente erweitert.
| Elemente | Vergleiche | Tauschoperationen |
| 5 | 10 | 4 |
| 10 | 45 | 22 |
| 100 | 4950 | 2464 |
| 1000 | 499500 | 243441 |
| 10000 | 49995000 | 25035918 |
Es ist zu beachten, dass diese Zahlen in anderen Implementierungen des BubbleSorts im Kleinen Abweichen koennen, jedoch bleibt der quadratische Zusammenhang der Vergleiche zu der Elementenanzahl. Die Tauschoperationen hängen vom konkreten Zustand der Datenmenge ab.
Nächste Seite: Implementierung
Aufwärts: BubbleSort
Vorherige Seite: Beispiel
Inhalt