Laufzeitkomplexität

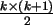Die Laufzeitkomplexität für den InsertionSort wird durch die Durchläufe und die Anzahl der Arbeitsschritte pro Durchlauf bestimmt. Insgesammt werden n - 1 Durchläufe durchgeführt, bei dem im worst case $\frac{k\times(k + 1)}{2}$, wobei k die aktuelle Markenposition darstellen soll (Gaussche Formel zur Berechnung der natürlichen Zahlen zwischen 1 und k). Eingesetzt und aufgelöst ergibt sich $\Rightarrow~\frac{n^2~-~n}{2}$ Arbeitsschritte im worst case, wobei n die Anzahl der Elemente in der zu sortierenden Menge bezeichnet. Die Abschätzung nach oben (worst case) der Laufzeitkomplexität für den InsertionSort ist somit: $O(n^2)$

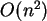
Der schlechteste Fall (worst case), also bei dem der InsertionSort wirklich $\Rightarrow~\frac{n^2~-~n}{2}$ Arbeitsschritte durchführen muss, entsteht dann, wenn die Datemenge in genau umgekehrter Richtung bereits vorsortiert ist, da jedes mal das Markenelement an den Anfang der bereits sortierten Menge geschaufelt werden muss.

Die folgende Tabelle zeigt die Anzahl der Vergleichs- und Tauschoperationen auf einer Datenemnge, welche mit Zufallszahlen gefüllt wurden, und bei jedem Test um zusätzliche Elemente erweitert wurde.

Elemente Vergleiche Tauschoperationen
5 7 6
10 24 18
100 2680 2592
1000 243948 242964
10000 25194592 25184610


Die gleichen Test wurden mit einer Datenemenge durchgeführt, die in umgekehreter Richtung vorsortiert war um den worst case für den InsertionSort zu simulieren. Sieht man sich die Vergleichszahlen an, findet sich dort die Formel der Arbeitsschritte wieder.

Elemente Vergleiche Tauschoperationen
5 10 10
10 45 45
100 4950 4950
1000 499500 499500
10000 49995000 49995000

Man beachte, dass die Anzahl der Tauschoperationen und der Vergleiche identisch sind. Dies rührt von der Tatsache, dass der InsertionSort das Markenelement bis nach ganz vorne in die Datenmenge einreiht und genauso viele Vergleiche durchführt.

Nächste Seite  Aufwärts  Vorherige Seite  Inhalt 


Nächste Seite: Implementierung Aufwärts: InsertionSort Vorherige Seite: Beispiel   Inhalt

2002-05-09