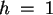Abstrakt

Wie schon erwähnt teilt der ShellSort die zu sortierende Menge und läßt den InsertionSort die Teilmengen abarbeiten. Die entstehenden Teilmengen sind jedoch nicht zusammenhängend und erfordern eine andere Implementierung des InsertionSorts als auf zusammenhängenden Mengen.

Genau genommen erfolgt keine Teilung sondern nur eine Auswahl von Elementen, die einer temporären, gedachten Menge zugeordnet werden, dabei sind die Elemente nicht benachbart. Die Auswahl fällt immer auf das h-te Elemente. Die so entstandene Auswahl wird sortiert; man spricht dann von h-Sortierung. In der Origianlmenge sind jedoch genau h Teilmengen, wenn man die Indizierung der Menge nicht mit 0 begint, sondern mit 1, mit 2, ...bis h - 1. Somit werden in einer Sortierstufe diese h Mengen sortiert.

Da die Elemente in der Originalmenge present ist, wird die Originalmenge bei der Sortierung der Teilmengen mitverändert. Die Vorgehensweise des ShellSorts äußert sich zunächst in einer sehr groben Teilung (große Werte für h). Nach Sortierung dieser durch die Selektion entstandenen (h) Mengen, geschieht wieder eine Selektion, diesmal mit einem kleineren Wert für h, und somit einer feineren Auswahl. Dies wiederholt sich zyklisch solange h größer 0 ist. Für den Fall 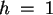$h~=~1$ gibt es auch nur eine temporäre Menge, die alle Elemente aus der Originalmenge enthält. Das Verfahren nach dem h verkleinert wird, also die Auswahl getroffen wird, hat Auswirkungen auf die Laufzeit des Algorithmus.

In einer Animation des ShellSorts wird ersichtichtlich, wie die gesammte Menge langsam einen sortierten Zustand annimmt, wobei sich nicht wie bei anderen Sortieralgorithmen zusammenhängende wirklich sortierte Mengen bilden. Vielmehr sieht es aus, als würde der ShellSort nur eine grobe Sortierung vornehmen. Dies geschieht aber über mehrere Iterationen hinweg immer genauer, was letztlich zu einer sortierten Originalmenge führt.

Da bei jeder Stuffe der Wert für h kleiner gesetzt wird, damit die Selektion feiner geschehen kann, stellt sich die Frage, nach welchem Prinzip dieses Verkleinern erfolgt. Die wohl einfachste und durchaus effiziente Weise ist die Teilung des Wertes h durch 3. Später sollen noch andere Formel vorgestellt werden.

Nächste Seite  Aufwärts  Vorherige Seite  Inhalt 


Nächste Seite: Beispiel Aufwärts: Arbeitsweise Vorherige Seite: Arbeitsweise   Inhalt

2002-05-09