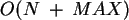Laufzeitkomplexität

Wie später bei der Implementierung zu sehen ist, besteht jeder Schritt des CountingSort aus einer einfachen Schleife. Alle Schleifen arbeiten weise eine Laufzeit von N, wobei es eine Ausnahme gibt. Diese ist das Aufsummieren der Häufigkeiten, was eine Komplexität von MAX aufweißt. Somit beläuft sich die Laufzeitkomplexität des Algorithmus auf $O(N~+~MAX)$. Dabei ist N die Anzahl der zu sortierenden Elemente und MAX der Wert des größten Elements.

Der Programmierer sollte sich dessen bewust sein, das der Speicherverbrauch unabhängig von der temporären Kopie für die Sortierung, der Speicherbedarf für das Häufigkeits-Array linear zum grössten Element wächst.

Der Algorithmus ist sehr gut geeignet für Datenmenge, die durchaus as vielen Elementen bestehen, diese jedoch nicht alzu unterschiedlich sind, und kein groses Extrema zwischen dem kleinsten und größten Elemente aufweisen. Er ist jedoch nicht stabil, das heißt er legt benachbarte gleiche Elemente nicht in der gleichen Reihenfolge ab, sondern in genau umgekehrter Richtung.

Nächste Seite  Aufwärts  Vorherige Seite  Inhalt 


Nächste Seite: Implementierung Aufwärts: CoutingSort Vorherige Seite: Arbeitsweise   Inhalt

2002-05-09