Wie schon angedeutet gibt es eine Variante des MergeSorts, welche ``in-place'' arbeitet, also
keinen zusätzlichen Speicher benötigt. Allerdings hat diese Methode den Nachteil der Laufzeit.
Wie so oft in der Informatik begegnet man hier dem Problem ``Speicher gegen Laufzeit''. Der einfachheitshalber
soll hier wieder der rekursive Ansatz hergenommen werden, um die ``in-place'' Variante zu realisieren.
Der entsprechende Code, der für das Mischen der Mengen verantwortlich ist, kann in eine separate Funktion
ausgelagert und z.B. in der nicht rekursiven Version benutzt werden.
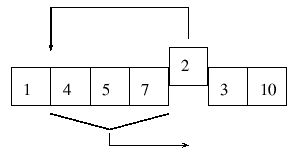
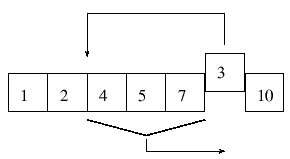
Der Trick beim Mischen ist, die Elemente wie gewohnt in eine Menge abzulegen, wobei diese allerdings die
Quellmenge selbst ist. Damit die ``alten'' von dem neuen Element nicht überschrieben werden, müssen
diese bis zu der Stelle nach hinten gerückt werden, an dem das ``neue'' Elemente residierte.
Dieses Verfahren hat zwar den Vorteil, keine zusätzlichen Speicher zu benötigen, jedoch wieder den Nachteil, die Laufzeit des gesamten
Algorithmus wesentlich zu verschlechtern. Dies rührt von der Tatsache das N Elemente im schlechtesten Fall M mal verschoben
werden müssen. Im obigen Beispiel wäre 3 Elemente, die 2 mal verschoben worden sind.
![\begin{listing}{1}
void inplace_merge_sort(
int * data,
int left,
int rig...
...eft] = tmp;
\par left++;
end_left++;
start_right++;
}
}
}
} \end{listing}](img44.png)
Nächste Seite
Aufwärts
Vorherige Seite
Inhalt
Nächste Seite: Laufzeitkomplexität
Aufwärts: Implementierung
Vorherige Seite: nicht rekursiv (iterativ)
Inhalt
2002-05-09


![\begin{listing}{1}
void inplace_merge_sort(
int * data,
int left,
int rig...
...eft] = tmp;
\par left++;
end_left++;
start_right++;
}
}
}
} \end{listing}](img44.png)